二次方程式の文章問題 道幅についての練習問題です。 解説記事はこちら gt;二次方程式の利用(文章問題)解き方まとめ スポンサーリンク 目次1 方程式練習問題二次方程式の文章問題~道幅について~2 練習問題の解所謂的預解式就是滿足某一預解形的方程式,並且此方程式的求解問題比原來方程式簡單。 Lagrange 曾經考慮五次一般方程式 x 5 a 1 x 4 a 2 x 3 a 3 x 2 a 4 xa 5 =0 ,令其五個根為 ,,,, ,並且 。考慮預解形 ,由此得到一個次數為 1 的預解式。 這個預解式可以表示成 x 5 的 24 次的方程式。然後次に類似した 5 個の問題 x^23x=28 x 2 − 3 x = 2 8

8年級上數學 資優題 一元二次方程式應用問題 17 12 30 Youtube
2次方程式 問題 簡単
2次方程式 問題 簡単-中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード・印刷 2次方程式の考え方と解き方の練習問題プリントです。 方程式の形に応じて、適切な解き方が出来るよう、「因数分解」「平方根の考え方」「解の公式」をそれぞれ使った3種類の方法を詳しく解説しました。若方程式的解可以由有限次 常見 丟番圖問題一般可以有數條等式,其數目比未知數的數目少;丟番圖問題要求找出對所有等式都成立的整數組合。用另一種語言來說,丟番圖問題定義代數曲綫或者代數曲面,或更爲一般的幾何形,要求找出其中的柵格點。對丟番圖問題的數學研究稱為 丟番圖
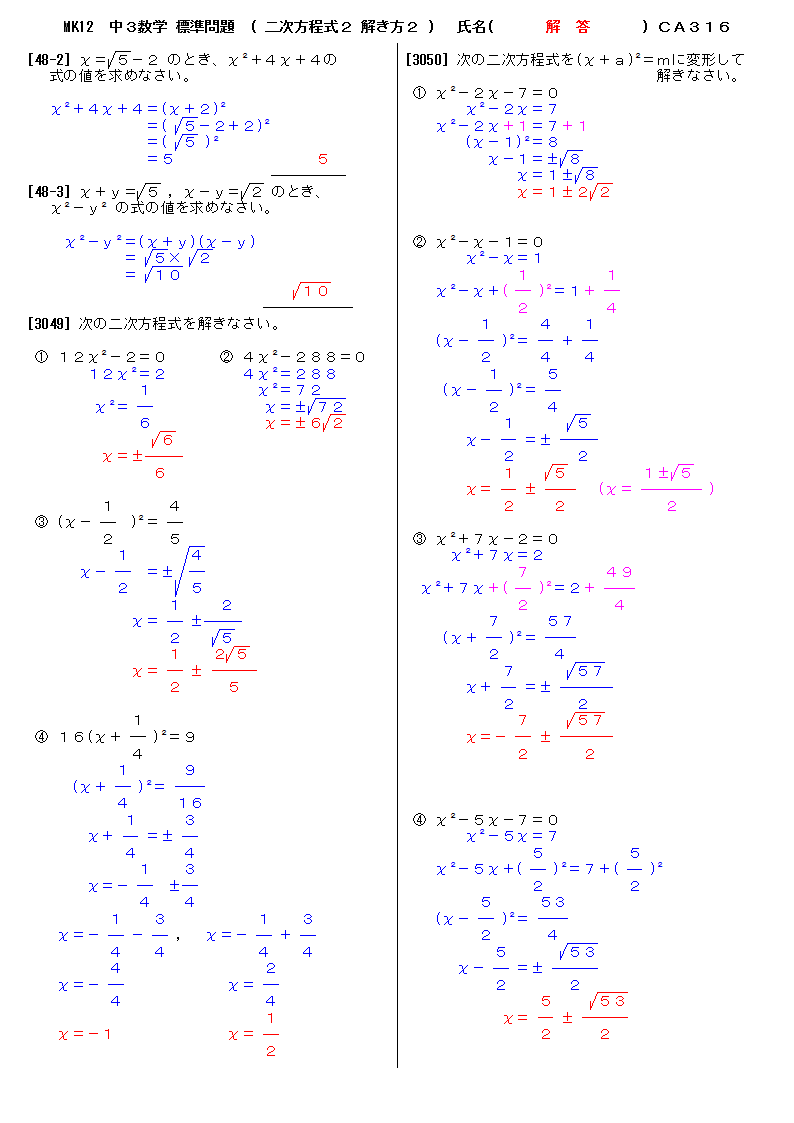



無料 中3数学 標準問題 解答プリント 316 2次方程式2 解き方2
2次方程式の文章題ー図形の問題 2次方程式の文章題の図形の問題です。 面積を求める問題が多く出題されます。 まず、分からないところをxとおいて、面積が等しくなる方程式を作ります。 2次方程式を解いて解を求めればいいのですが、正の数の解でも解答になるとは 16年9月4日2次方程式の解を使った問題 問題 x 2 x 1 = 0 の解をα,βとするとき α 3 β 3 の値を求めよ。 ベビクマ 因数分解して解がすぐに出せなさそうだから、解の公式を使えばいいのかあ? でも面倒く2次方程式 (x2) (x−2)=2 (3x−2) を解きなさい。 両辺に式があるような二次方程式は,展開・整理して式を左辺に集めてから考えます. 前問と同様に, x=0 を忘れないように気を付けましょう. 方程式 x 2 −2x−35=0 を解きなさい。 左辺が因数分解できる二次
現在我們要利用朗斯基行列式以及二階線性微分方程式初始值問題解的存在性一性證 明 二階線性齊次微分方程式 (不指定初始值條件) 解空間的維度是 2。 定理 7 (第112 頁) 如果 y1(x) 與y2(x) 是二階線性齊次微分方程式 (3) 的解, 而且在 某個點x0 ∈I上的朗斯基行列式 Wy1,y2(x0) 6= 0 , 則所有微分方程式 2次方程式の文章題の発展問題を扱う。 このあたりは、学校準拠教材や標準レベルの入試問題集ではほとんど練習の機会がない。 前回 ←2次方程式の文章題(1)(代入、数量関係、面積体積)(基~標) 次回 → xの二乗に比例する関数(基) 諸事情でかなり遅れてしまった・・・やっと次回から2次二次方程式の利用 箱の容積 まとめ お疲れ様でした! 二次方程式の箱の容積を考える文章問題は 定期テストでは必須の問題です。 必ず解けるようにしておきましょう。 ポイントは このように、それぞれの辺を を用いて表せるかどうかですね。 文字
Title FdData中間期末過去問題中学数学3年(二次方程式応用/係数/数/面積・体積/動点) Author Fd教材開発 Created Date(2) 2、1、0、1、2のうち、二次方程式 t 6 f t2 l0の解は どれか。 (3) 次の二次方程式で5が解であるものを選び、記号で答えなさ い。 (ア) t 65 t3 l0 (イ) t 65 (4) 次の二次方程式で1と5が解であるものを選び、記号で答え なさい。 (ア) t e1 ;608~ 第2問(x, y, z )一夜漬け高校数学~一夜漬けでの小さな努力で大きな成果を出すためのいくつかの提案~※睡眠は記憶効率をアップさ




109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass



解一元二次方程式之應用問題 Live 多媒體數學觀念典online
ディオファントス方程式(ディオファントスほうていしき、Diophantine equation)とは、整係数多変数高次不定方程式である。 文脈として、整数解や有理数解を問題にしたい場合に用いられる用語であり、主に数論の研究課題と考えられている。 古代アレクサンドリアの数学者 ディオファントスの 二次方程式の応用問題です。 それではどうぞ。 右の I図 のように1辺が1cmの正方形の白色と黒色タイルがある。 これを II図 のようにある規則に従って, 隙間なく並べていく。 このとき次の問いに答えなさい。 (1) 番目の図形には, 1辺1cmの白色のタイルは 食塩水の濃度の問題(2次方程式) 投稿日 年5月19日 年12月12日 100sai 食塩水と濃度(濃さ)の関係は次のようになります。 食塩水の重さ= 食塩の重さ 水の重さ 食塩水の濃度 (%)=食塩の重さ 食塩水の重さ 食塩の重さ= 食塩水の重さ×



Q Tbn And9gcskwhhvvfmhhhoiqlmko5jaa7cw6bcheq Snuulphiez3ruztc6 Usqp Cau



初中数学知识点总结 二次函数的应用 学习云课堂
2次方程式の接線の求め方を解説! 21年4月22日 二次方程式の接線ってどうやって求めるの? さっそくですが、こんな問題見たことありませんか? 今回の課題1 次の関数のグラフ上の点Aにおける接線の方程式を求めよ。 こんな問題とか 今回の課題2 次の 今回は、前回より難しい2次方程式の解き方を見ていく このレベルまでできれば、十分ではある。 前回 2次方程式の解き方と練習問題(1)(基) 次回 2次方程式の解き方(3)(難)Title 2次方程式の徹底100問 Author 4278 Last modified by 奥 淳 Created Date AM Other titles 2次方程式の徹底100問




三元二次方程 三元二次方程是指有三個未知數 最高次數為二次的方程 一般 百科知識中文網




年中考数学必考考点 一元二次方程及其应用 初中数学知识点概念大全练习题 哔哩哔哩
這個問題很簡單,我們剛剛代入的 = 就是其中一個答案,但是我們想問的是:還有沒有其他答案? 如果沒有測試過,我們想知道在 x {\displaystyle x} 是多少的情況下,式子 2 x 7 {\displaystyle 2x7} 的值剛好是 10 {\displaystyle 10} ?2 2 2 次方程式 a x 2 b x c = 0 ax^2bxc = 0 ax2 bx c = 0 ( a ≠ 0 a \neq 0 a = 0 )の解は x = − b ± b 2 − 4 a c 2 a x = \frac {b\pm\sqrt {b^24ac}} {2a} x = 2a−b ± b2 − 4ac問題1 次の空欄を埋めよ.なお,答が負の分数になるときは,分子を負の数にして答えよ. 採点する ただし,「2次方程式の解の公式」からは,無理数解や虚数解が出る場合もあるので,「複素数の係数まで使えば,どんな2次式でも因数分解できる」という意味になる. 例題 次の式を複素




二次方程式の解き方のまとめ 中学生に覚えてほしいパターンは5つ 中学や高校の数学の計算問題
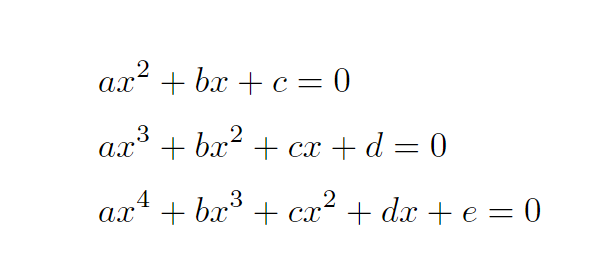



关于二次 三次 四次方程求解方法讨论 知乎
速度と距離の問題(1次方程式) 投稿日 年2月12日 年12月8日 100sai 方程式を利用して問題を解くときには、問題文の中のどれかひとつの量を\(~x~\)として、他の量を\(~x~\)を使って表し、それらの量の関係を満たす方程式をつくります。練習問題4 次の方程式を解きなさい。 1 3( x -5)=2-4(2 x -4) 2 4(2 x -1)-5=3 x -2(5 x +3) 3 11 x -{3 x +4(3 x -1)}=0 4 27-{3 x -5( x -3)}=-6 x << L16 一次方程式の計算(2) の問題に戻る L17 一次方程式の計算(3) の解答表示 >> 中1数学・練習問題二次方程式の解き方はバッチリになりましたか? 二次方程式は解き方がたくさんあるので、ちょっと難しく感じる方もいるかもしれません。 苦手な方は、とにかく演習あるのみです! 問題を眺めているだけでは、解き方は身につきません。
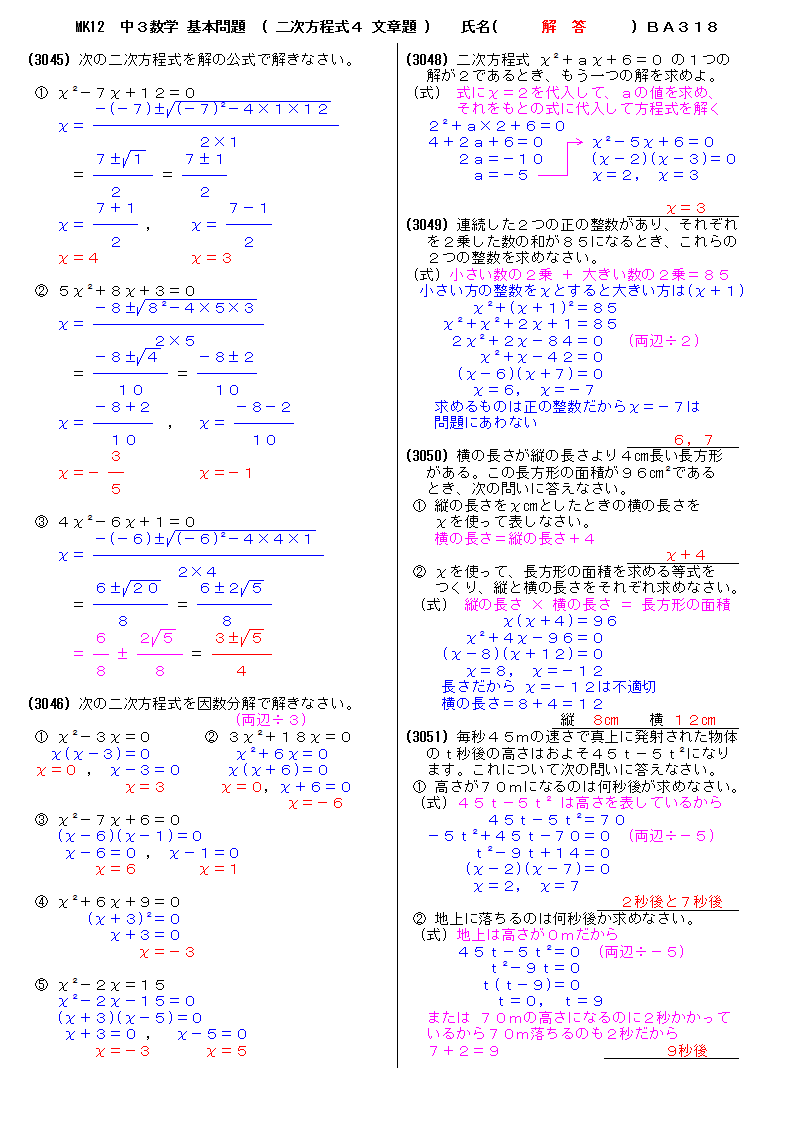



無料 中3数学 基本問題 解答プリント 318 2次方程式4 文章問題




1 次方程式文章題 ニスヌーピー壁紙
今回は2次方程式の問題演習です。 全部解くことが出来たら、この単元を十分理解していると言っても過言ではありません! では、今回も頑張っていきましょう! あすなろには、毎日たくさんのお悩みやご質問が寄せられます。 この記事は数学の教科書の採択を参考に中学校3年生のつまずき基本的に中学校で出題される2次方程式の問題はすべて平方完成で解くことができます。 ただ、因数分解できる2次方程式は因数分解で解く方が簡単なので、因数分解できない問題を平方完成するのが基本となります。 平方完成を利用した2次方程式の解き方 今回は例題として \(x^24x6=0\) を平方数学33章二次方程式「二次方程式の利用」<準備問題①> 組 番 名前 次の方程式を解きなさい。 (1)3χ2-15=0 (2)(χ+7)2-18=0 (3)χ 2+10χ+24=0 (4)χ-12χ+35=0 (5)χ 2-χ-72=0 (6)χ+19χ=0 (7)χ2-18χ+81=0 (8)3χ2+9χ+2=0 (9)χ 2-3χ+1=0 (10)χ-6χ+2=0 5 2 57 5 7 5 18 32 2 6 2 2 2 2 2 数�



問題 數學問題一元二次方程式 校園生活哈啦板 巴哈姆特




数学問題 意外と間違える人が多い二次方程式の基本問題 暇つぶしに動画で脳トレ
MathAquarium練習問題+解答2 次関数 2 2 (1) 放物線y=-2x2-14x-13 をどれだけ平行移動すると,放物線y=-2x2+8x+7 に重なるか。 (2) 2 次関数y=x2+ax+4 のグラフを,x 軸方向に2 だけ平行移動すると2 次関数y=x2-9x+b の グラフとなる。このとき,a,b の値を求めよ。在這基礎,方程式求解問題的研究在宋金元時代達到最高峰。其代表人物是秦九韶(12~1261,南宋人)、李冶(1192~1279,金末元初人)和朱世傑(約1260~13,元人)。他們的主要成就是,聯立同餘方程式,一元高次方程式的近似根,立方程解問題的代數學方法,多元高次聯立方程式 。 101 聯問題解決の場面で活用できるようにし,方程式をこれまでより多くの場面で問題の解決に活用 できるようにする。 2 ・二次方程式の意味を知る。 ・二次方程式の解と二次方程式を解くことの意 味を知る。 ・二次方程式とその解の意味を理解する。 (知識,理解・ノート) ・二次方程式の



Q Tbn And9gcrwr5k W1f2iibd39mbbjyhda5ozoo5bwykspo4weqwhlvaeg X Usqp Cau




一元二次方程式 懶人包




二次方程式




解一元二次方程式 明誠中學程式設計學習網



學習數學的迷思 記憶與背公式 以二次方程式及不等式為例 這是小蜜蜂文理美術補習班的部落格 隨意窩xuite日誌




2次方程式の解と係数の決定 無料で使える中学学習プリント
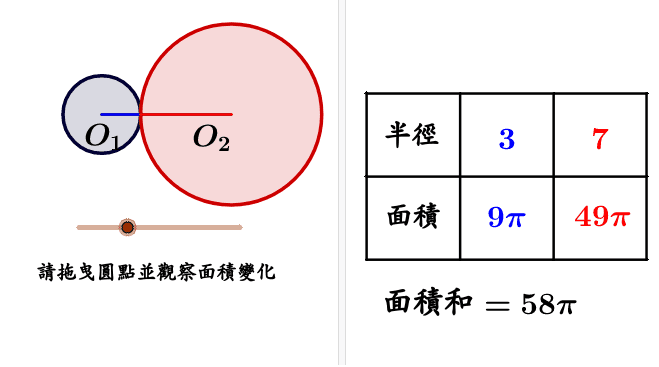



一元二次方程式 應用問題 兩圓相切 2 Geogebra




09增长率问题一元二次方程初中数学初三 Youtube
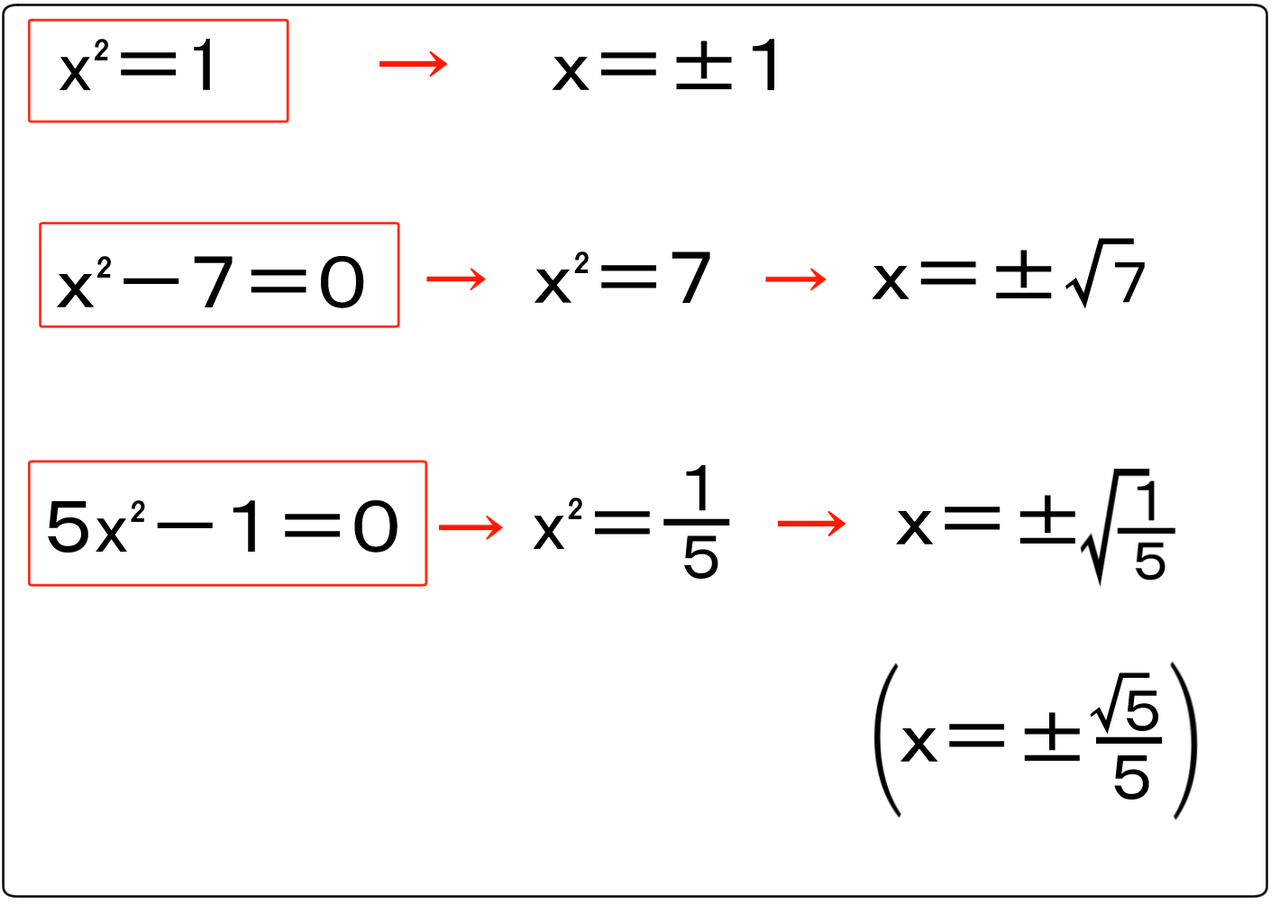



2次方程式 2 どの方法で解けばいいの バカでもわかる 中学数学



Http Www2 Chsh Chc Edu Tw Bee 104 a Pdf




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




二元二次方程的解法 知乎




0以上2 次方程式問題 シモネタ



一元二次方程配方法 4道提高题 全做对你就是学霸水平 初中 Qq教育网



初中数学知识点总结 一元二次方程的应用 易贤网




一道计算一元二次方程解的算法题 Sesiria的博客 Csdn博客




一元二次方程式應用問題 例4 5 6 均一教育平台




二次方程式の利用 チーム エン



求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博




中3 中3数学 2次方程式 中学生 数学のノート Clear




二次方程式の解がわかっている問題は xに代入して計算しよう 中学や高校の数学の計算問題



23 2 一元二次方程的解法 5 修订版教案 Rar 华九上 22 2一元二次方程 的解法 初中华师大版13版 数学中国网 Mathschina Com




2次方程式の解の配置問題 おいしい数学




8年級上數學 資優題 一元二次方程式應用問題 17 12 30 Youtube




一元二次方程式應用問題 例3 已下架內容 均一教育平台




初中数学一元二次方程求根公式 一元二次方程的解法 一元二次方程根与系数的关系 101教育知识点频道手机端
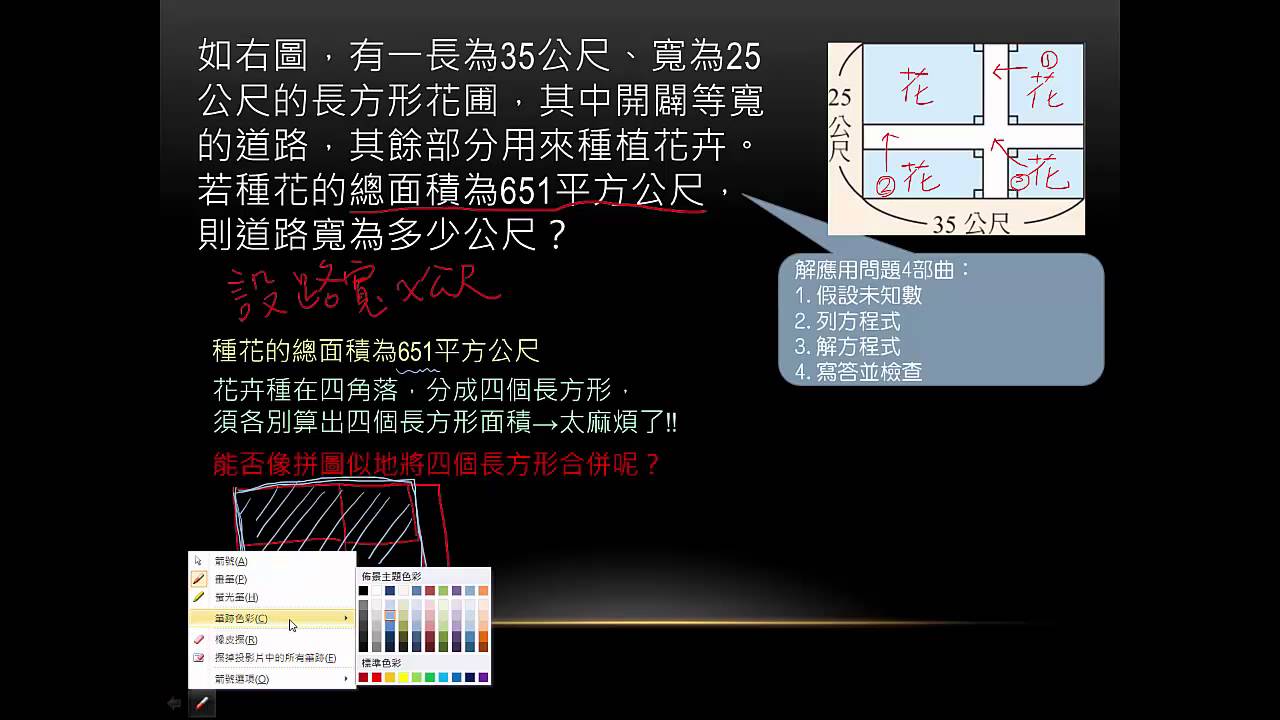



翻轉學習影片 國中 數學 12 2 2 一元二次方程式的應用問題




中学数学 二次方程式




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
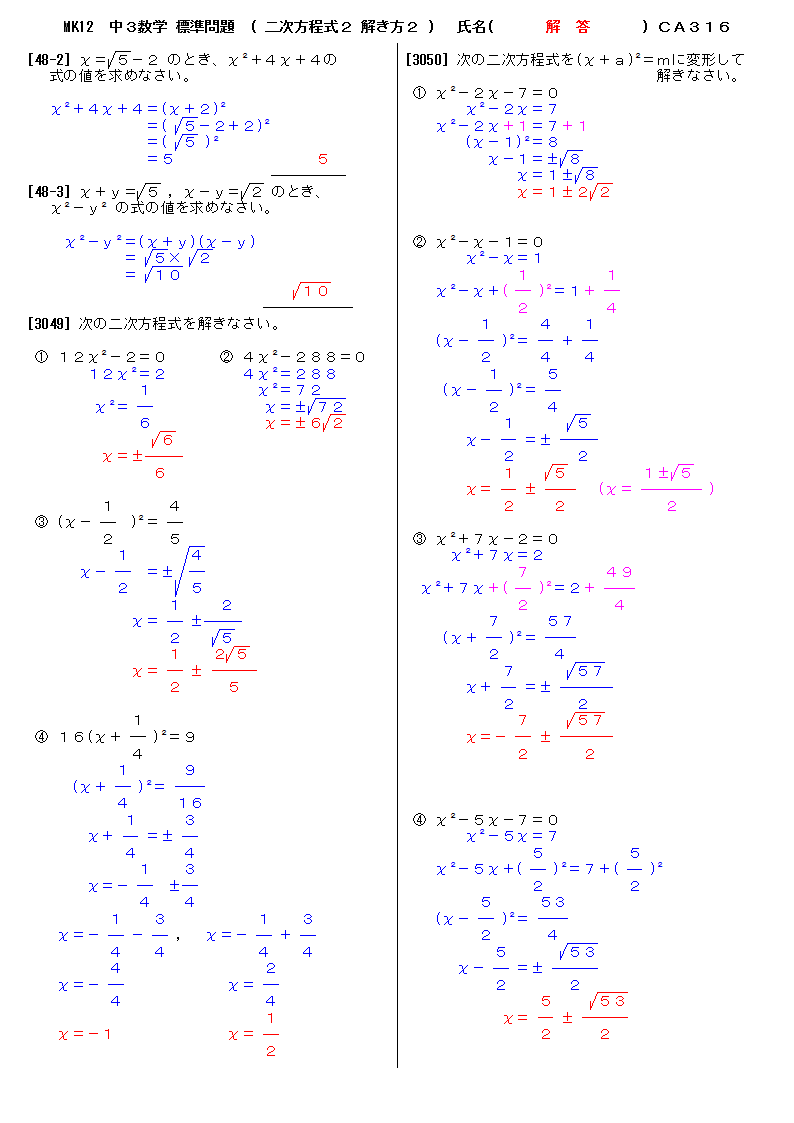



無料 中3数学 標準問題 解答プリント 316 2次方程式2 解き方2




最も欲しかった 数学2 次方程式 ニスヌーピー壁紙
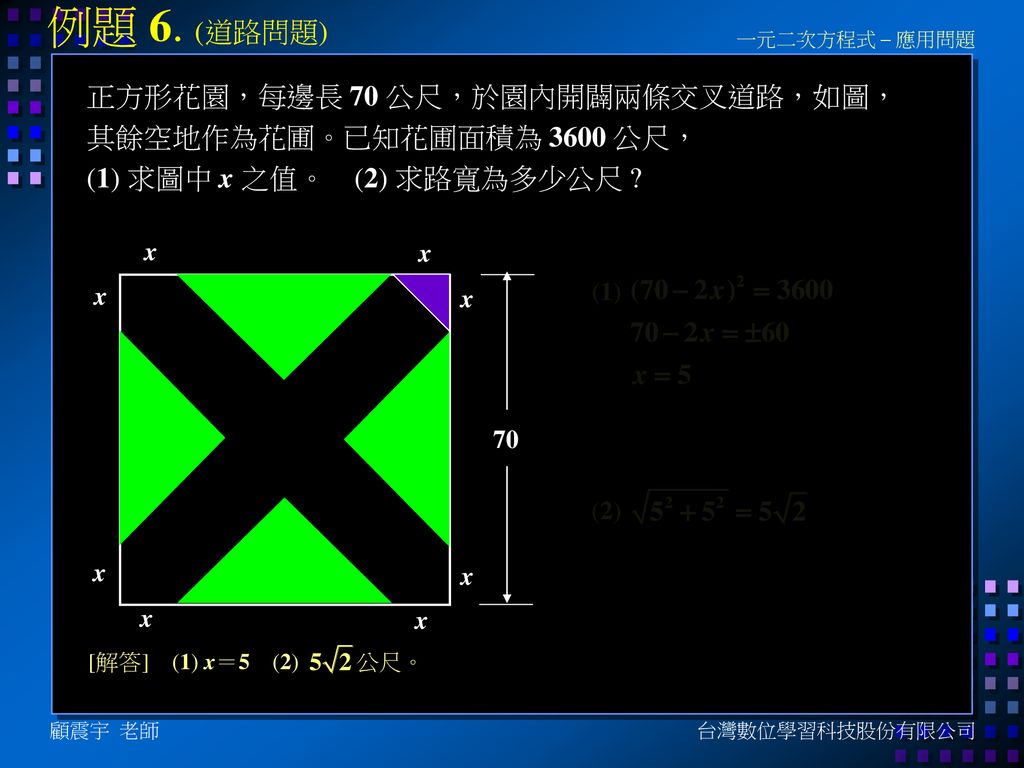



一元二次方程式 應用問題 顧震宇台灣數位學習科技股份有限公司 Ppt Download




世界一わかりやすい数学問題集中3 3章 二次方程式




如何求解四度方程 自然科学21




中学数学 二次方程式




2次方程式の文章題ー図形の問題 無料で使える中学学習プリント



高中常见题 解三元二次方程组 哔哩哔哩 つロ干杯 Bilibili




亿源老师教案发表 配方法解一元二次方程式 备课吧




二次方程式で解の公式を使う問題 見分け方は因数分解がポイント 中学や高校の数学の計算問題



试题库 一元二次方程选择压轴挑战题 潍坊中考 家长帮



Q Tbn And9gctivnh0ytvm5iq2nnhaeu2fa7uykcwky0 V7mocdeysfgddbodx Usqp Cau




基測數學 98v2 單選34 一元二次方程式的應用問題 Youtube




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



二次方程式の利用 文章問題 解き方まとめ 方程式の解き方まとめサイト




無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア




二次方程式の利用 スタディーx




中考 一元二次方程解應用題 題型總結 轉給需要的同學吧 壹讀




有人會嗎一元二次方程式的應用問題 Clear




世界一わかりやすい数学問題集中3 3章 二次方程式




1916北興國中三軌學思達公開課講義 數學 英文 Shareclass



一元二次方程考点透视 第52周 综合复习 初中人教五四制 数学中国网




2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学



中3数学 二次方程式の解き方と因数分解 解の公式の覚え方と簡単な計算問題 猫に数学




0以上2 次方程式問題 シモネタ
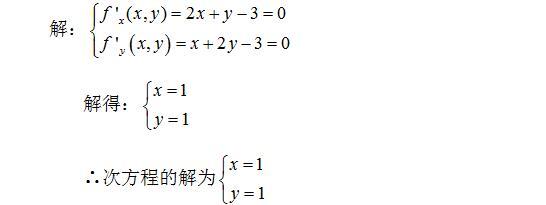



二元二次方程的解法 知乎



名師課輔網 數學一元二次方程式的應用




愛學網播放影片



中学数学単元別 2次方程式 数学中学校教材問題集 Buyee 日本代购平台 产品购物网站大全 Buyee一站式代购bot Online




一元二次方程應用題總結分類及經典例題 每日頭條



請益用excel 解一元二次方程式 課程板 Dcard




2次方程式の応用問題の解き方 文章問題 数学fun




0以上2 次方程式問題 シモネタ



求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博




一元二次方程的虚数根 一元二次方程的虚根怎么算 三人行教育网 Www 3rxing Org



解一元二次方程及不等式练习题 Doc 沃文网wodocx Com



求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博
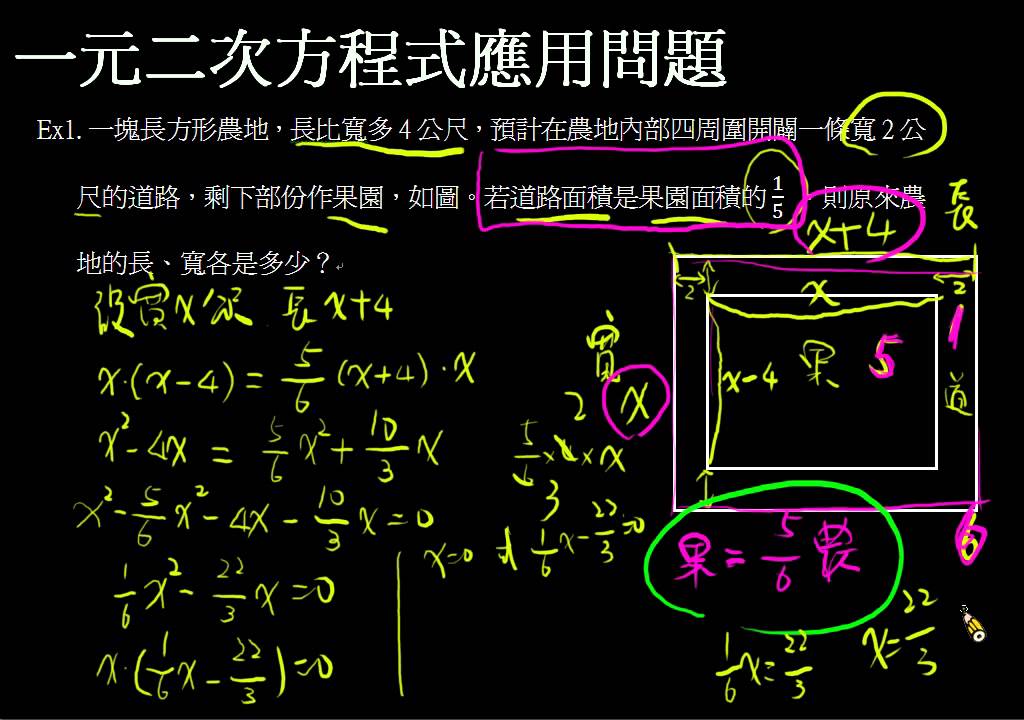



一元二次方程式應用問題 例1 2 Youtube




109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass




一元二次方程的實際應用 常見應用題的解題方法及步驟 每日頭條




2次方程式 2 どの方法で解けばいいの バカでもわかる 中学数学




中学3年数学 二次方程式 解の公式 確認問題2 あんのん塾




翻轉學習影片 國中 數學 一元二次方程式 一元二次方程式應用問題 練習2
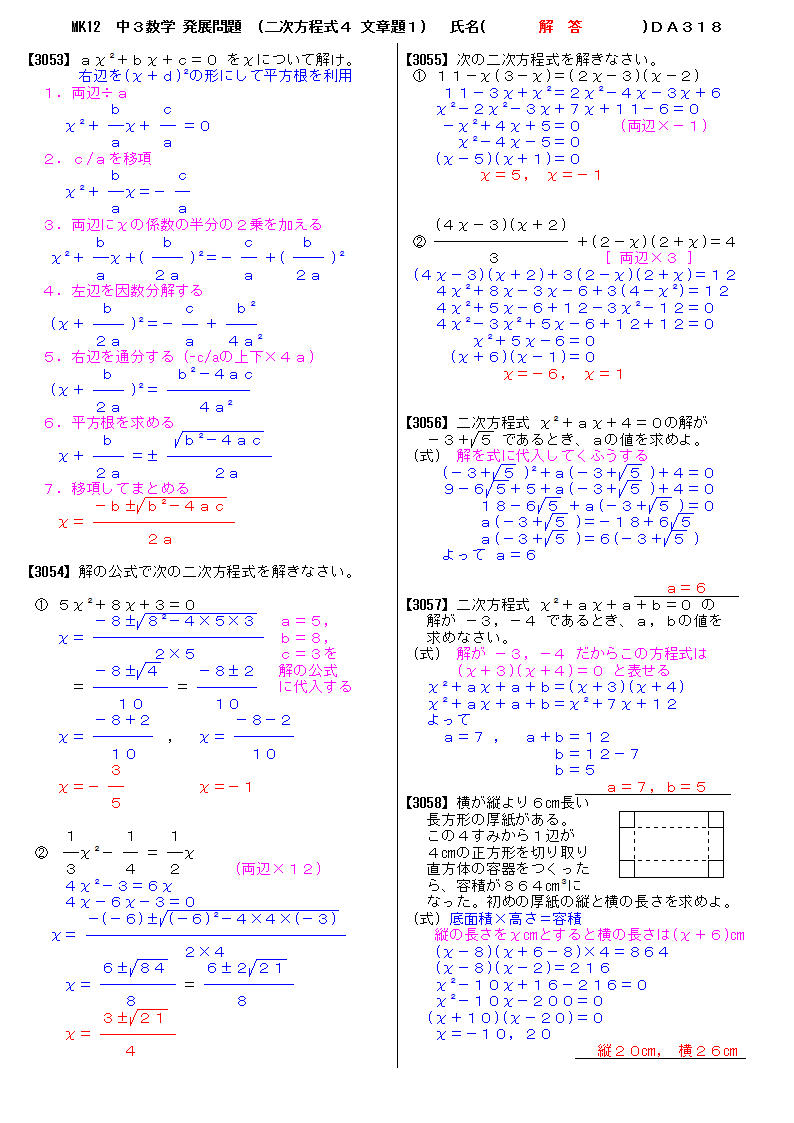



無料 中3数学 発展 応用問題 解答プリント 318 2次方程式4 文章問題1



一元二次方程练习题精选一 初三数学 中考网




这几类一元二次方程应用题不会 中考考高分难了 热点题 楠木轩



初中数学知识点总结 一元二次方程的应用 学习云课堂




二元二次方程組的解法 每日頭條




用公式解解一元二次方程式 Youtube




一元二次方程式應用問題 例7 8 已下架內容 均一教育平台
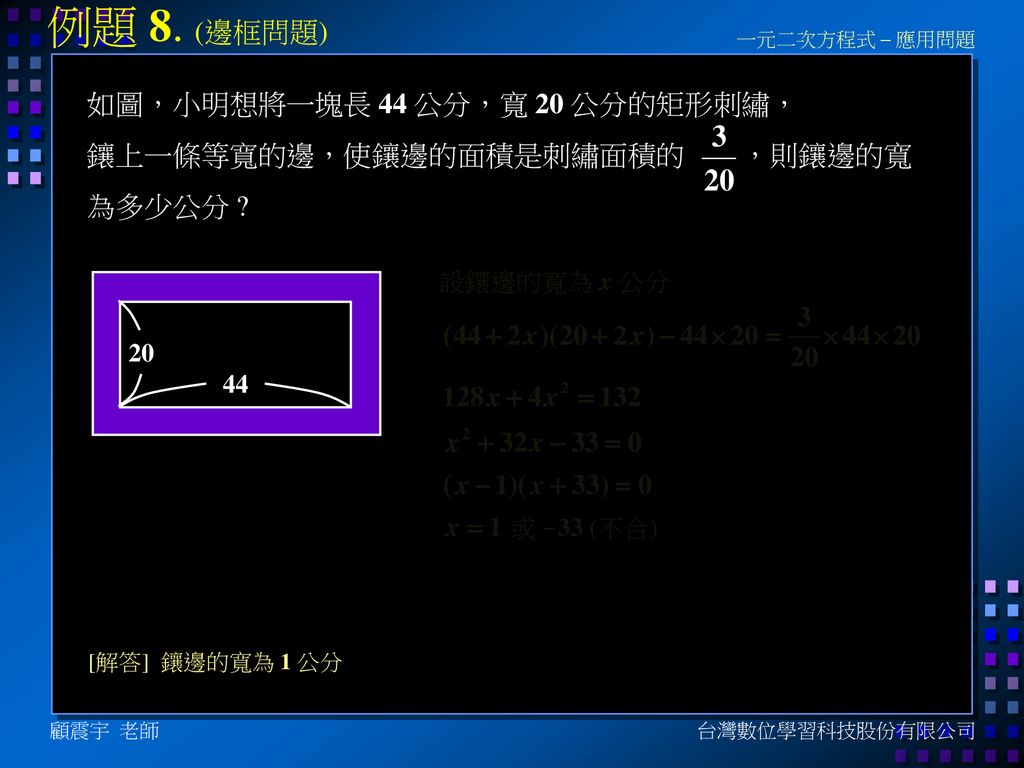



一元二次方程式 應用問題 顧震宇台灣數位學習科技股份有限公司 Ppt Download




例題 利用配方法解一元二次方程式2 二次項係數不為1 數學 均一教育平台




作業成果 配方法解一元二次方程式 Hahow 好學校




年中考数学必考考点 一元二次方程及其应用 初中数学知识点概念大全练习题 哔哩哔哩




北师大版九年级数学上思维特训 七 含答案 一元二次方程根与系数关系的运用技巧 七七文库www 77wenku Com




中学3年生 数学 2次方程式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



韦达定理 一元二次方程根与系数的关系 科普中国



一元二次方程 面积类应用题 4种重要题型详细分析



Q Tbn And9gctgoae9bomuk0gymqhrkjzep3izucoijhp9evjmecua8k 13ra4 Usqp Cau



一元二次方程的应用题 十五种必考题型总结




五次方程 维基百科 自由的百科全书




初中數學 一元二次方程的常見考點 你都掌握了哪些 每日頭條



解一元二次方程及不等式练习题 Doc 沃文网wodocx Com



0 件のコメント:
コメントを投稿